Кодирование информации и избыточность кода
Любое сообщение, может быть представлено в различной форме, то есть закодировано различными способами. Разные способы кодирования неравноценны по занимаемому ими количеству информации.
Оптимальным кодом будет тот, при использовании которого среднее значение энтропии, приходящееся на один символ, равно энтропии источника информации.
В большинстве случаев используемые системы кодирования обладают избыточностью, то есть требуют для записи большее количество информации, чем оно содержится в кодируемом сообщении. Избыточность определяется формулой \[E = 1 - \frac{H}{Q}\] где \(H\) - энтропия сообщения, \(Q\)- среднее количество информации, приходящееся на один символ кодированного сообщения.
Чем выше избыточность кода, тем больше вероятность безошибочной передачи информации, но тем больший объём требуется для её хранения и большая пропускная способность канала передачи. Естественные человеческие языки характеризуются очень высокой степенью избыточности, также велика избыточность генома высших организмов, хранящегося в молекулах ДНК.
Величина \(H /Q\) называется экономичностью кода. Для оптимального кода \(H /Q=1\) а избыточность отсутствует, то есть \(E = 0\).
Процесс уменьшения избыточности кодирования называется сжатием информации и применяется для понижения объёма памяти, требуемой для хранения информации. Для сжатия информации, хранящейся в памяти, используются– архиваторы и упаковщики.
Пример: определить энтропию информации, содержащейся в сообщении «ученье − свет, а не ученье – тьма» и избыточность кода. Каждый символ в сообщении кодируется 1 байтом (8 бит).
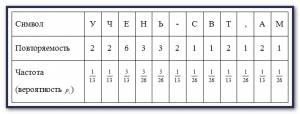
Решение: Подсчитаем количество символов в сообщении, для простоты игнорируя пробелы: N=26. Найдём частоту повторения каждого символа (вероятность в сообщении), составив следующую таблицу, приведенную на скрине слева.
Удельная энтропия (энтропия одного символа в сообщении) в битах на символ, равна \[\tilde H = 5 \cdot \frac{1}{{13}}{\log _2}13 + \frac{3}{{13}}{\log _2}\frac{{13}}{3} + 2 \cdot \frac{3}{{26}}{\log _2}\frac{{26}}{3} + 4 \cdot \frac{1}{{26}}{\log _2}26 \approx \] \[ \approx \frac{5}{{13}} \cdot 3.7004 + \frac{3}{{13}} \cdot 2.1155 + \frac{6}{{26}} \cdot 3.1155 + \frac{4}{{26}} \cdot 4.7004 \approx 3.3535\] Полная энтропия сообщения \(H = 3.3535 \cdot 26 = 87.19\) бит. Количество бит, необходимое для кодирования каждого символа одним байтом, составляет \(Q = 208\;\) бит.
Избыточность кода \(E=1-87.19/208=0.58=58%\).
В большинстве случаев используемые системы кодирования обладают избыточностью, то есть требуют для записи большее количество информации, чем оно содержится в кодируемом сообщении. Избыточность определяется формулой \[E = 1 - \frac{H}{Q}\] где \(H\) - энтропия сообщения, \(Q\)- среднее количество информации, приходящееся на один символ кодированного сообщения.
Чем выше избыточность кода, тем больше вероятность безошибочной передачи информации, но тем больший объём требуется для её хранения и большая пропускная способность канала передачи. Естественные человеческие языки характеризуются очень высокой степенью избыточности, также велика избыточность генома высших организмов, хранящегося в молекулах ДНК.
Величина \(H /Q\) называется экономичностью кода. Для оптимального кода \(H /Q=1\) а избыточность отсутствует, то есть \(E = 0\).
Процесс уменьшения избыточности кодирования называется сжатием информации и применяется для понижения объёма памяти, требуемой для хранения информации. Для сжатия информации, хранящейся в памяти, используются– архиваторы и упаковщики.
Пример: определить энтропию информации, содержащейся в сообщении «ученье − свет, а не ученье – тьма» и избыточность кода. Каждый символ в сообщении кодируется 1 байтом (8 бит).Решение: Подсчитаем количество символов в сообщении, для простоты игнорируя пробелы: N=26. Найдём частоту повторения каждого символа (вероятность в сообщении), составив следующую таблицу, приведенную на скрине слева.
Удельная энтропия (энтропия одного символа в сообщении) в битах на символ, равна \[\tilde H = 5 \cdot \frac{1}{{13}}{\log _2}13 + \frac{3}{{13}}{\log _2}\frac{{13}}{3} + 2 \cdot \frac{3}{{26}}{\log _2}\frac{{26}}{3} + 4 \cdot \frac{1}{{26}}{\log _2}26 \approx \] \[ \approx \frac{5}{{13}} \cdot 3.7004 + \frac{3}{{13}} \cdot 2.1155 + \frac{6}{{26}} \cdot 3.1155 + \frac{4}{{26}} \cdot 4.7004 \approx 3.3535\] Полная энтропия сообщения \(H = 3.3535 \cdot 26 = 87.19\) бит. Количество бит, необходимое для кодирования каждого символа одним байтом, составляет \(Q = 208\;\) бит.
Избыточность кода \(E=1-87.19/208=0.58=58%\).
Похожие публикации: