Рекурсия в JavaScript на примере вычисления факториала
Можно долго спорить о том, стоит ли использовать рекурсию или не стоит. Иногда ее применение просто необходимо, а иногда совсем не оправдано. Все программисты знают, что с одной стороны рекурсия имеет свои преимущества, но и недостатков у нее тоже куча. Сейчас не об этом. Рассмотрим как можно применять рекурсию в JavaScript. И, безусловно, в качестве тестового примера будем юзать вычисление факториала. Если кто еще до сих пор не в курсе, то вот вам формула для вычисления факториала числа:
\[n!=1\times2\times3\times...\times n\]
К примеру:
\[6!=1\times2\times3\times4\times5\times6=720\]
Факториал числа 6 для этого примера можно вычислить без применения рекурсии. Например вот так:
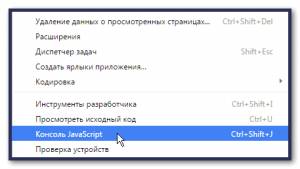 Для тех кто еще только начинает изучать JavaScript поясним, что результат работы скрипта для данного примера можно посмотреть в консоли JavaScript. Слева на картинке пример меню в Chrome для вызова консоли. Или можно нажать соответствующее сочетание клавиш. И в завершение, хотелось бы напомнить, что при реализации рекурсивных программ следует предусматривать надежный выход из рекурсии, чтобы не допустить зацикливания. Часто одного условия не достаточно, особенно в тех случаях, когда результат, получаемый от работы скрипта заранее не известен или условие выхода из рекурсии может оказаться недостижимым.
Для тех кто еще только начинает изучать JavaScript поясним, что результат работы скрипта для данного примера можно посмотреть в консоли JavaScript. Слева на картинке пример меню в Chrome для вызова консоли. Или можно нажать соответствующее сочетание клавиш. И в завершение, хотелось бы напомнить, что при реализации рекурсивных программ следует предусматривать надежный выход из рекурсии, чтобы не допустить зацикливания. Часто одного условия не достаточно, особенно в тех случаях, когда результат, получаемый от работы скрипта заранее не известен или условие выхода из рекурсии может оказаться недостижимым.
var factor = function(number) {
var result = 1;
var count;
for (count = number; count > 1; count--) {
result *= count;
}
return result;
};
console.log(factor(6));
// 720var countdown = function(value) {
if (value > 0) {
console.log(value);
return countdown(value - 1);
} else {
return value;
}
};
countdown(6);var factorial = function(number) {
if (number <= 0) { // terminal case
return 1;
} else { // block to execute
return (number * factorial(number - 1));
}
};
console.log(factorial(6));
// 720 Для тех кто еще только начинает изучать JavaScript поясним, что результат работы скрипта для данного примера можно посмотреть в консоли JavaScript. Слева на картинке пример меню в Chrome для вызова консоли. Или можно нажать соответствующее сочетание клавиш. И в завершение, хотелось бы напомнить, что при реализации рекурсивных программ следует предусматривать надежный выход из рекурсии, чтобы не допустить зацикливания. Часто одного условия не достаточно, особенно в тех случаях, когда результат, получаемый от работы скрипта заранее не известен или условие выхода из рекурсии может оказаться недостижимым.
Для тех кто еще только начинает изучать JavaScript поясним, что результат работы скрипта для данного примера можно посмотреть в консоли JavaScript. Слева на картинке пример меню в Chrome для вызова консоли. Или можно нажать соответствующее сочетание клавиш. И в завершение, хотелось бы напомнить, что при реализации рекурсивных программ следует предусматривать надежный выход из рекурсии, чтобы не допустить зацикливания. Часто одного условия не достаточно, особенно в тех случаях, когда результат, получаемый от работы скрипта заранее не известен или условие выхода из рекурсии может оказаться недостижимым.
Похожие публикации:
