Метод наименьших квадратов, МНК - онлайн

Пусть имеются результаты измерений (экспериментальные данные) двух величин. Если в системе координат на плоскости построить точки для пар измеренных данных и эти точки приблизительно выстраиваются по некоторой прямой или кривой, то это означает, что можно через эти точки провести некую линию, которая приблизительно будет описывать полученную зависимость.

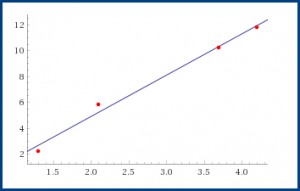Применяя метод наименьших квадратов можно найти уравнение линии, наилучшим образом, аппроксимирующую эти данные. На рисунке слева приведен пример такого построения для линейной зависимости (построены точки и прямая). Для решения такой задачи используют метод наименьших квадратов - МНК. Воспользуемся для этого нашим решателем - достаточно ввести специальную команду и набор координат точек. Ниже приведен пример такой команды для линейной зависимости (нажмите на кнопку вставки кода в решатель) и нажмите кнопку "Решить".

linear fit {1.3, 2.2},{2.1, 5.8},{3.7, 10.2},{4.2, 11.8}

Для квадратичной зависимости используют команду:

quadratic fit {10.1,1.2},{12.6, 2.8},{14.8,7.6},{16.0,12.8},{17.5,15.1}

Для нахождения кубической кривой используют следующую команду:

cubic fit 20.9,23.2,26.2,26.4,16.3,-12.2,-60.6,-128.9